A foundational result in machine learning is that a single-layer perceptron with N2 parameters can store at least 2 bits of information per parameter (Cover, 1965; Gardner, 1988; Baldi & Venkatesh, 1987). More precisely, a perceptron can implement a mapping from 2N, N-dimensional, input vectors to arbitrary N-dimensional binary output vectors, subject only to the extremely weak restriction that the input vectors be in general position.
….Wait what? Foundational? Was this in the Coursera Course?!
This short passage comes from Capacity and Trainability in Recurrent Neural Networks, a paper exploring empirically the nature of Recurrent Neural Networks. Their exploration extends much earlier work done to study simple single-layer perceptron networks, and it is from that decades old work that this “foundational result” comes.
So, I found this passage quite dense when I first read it. The following questions featured immediately and prominently:
- What does it mean for a network parameter to “store information”?
- What is “general position”?
- How does the implementation of that mapping from inputs to outputs entail “2 bits of information per parameter”?
- Why are there 3 references from physics journals? They talk about a Spin Glass. What’s that?
I didn’t get it, but this is apparently a foundational result, so off I went trying to.
a single-layer perceptron with N2 parameters … can implement a mapping from 2N, N-dimensional, input vectors to arbitrary N-dimensional binary output vectors…
The network described looks like this:
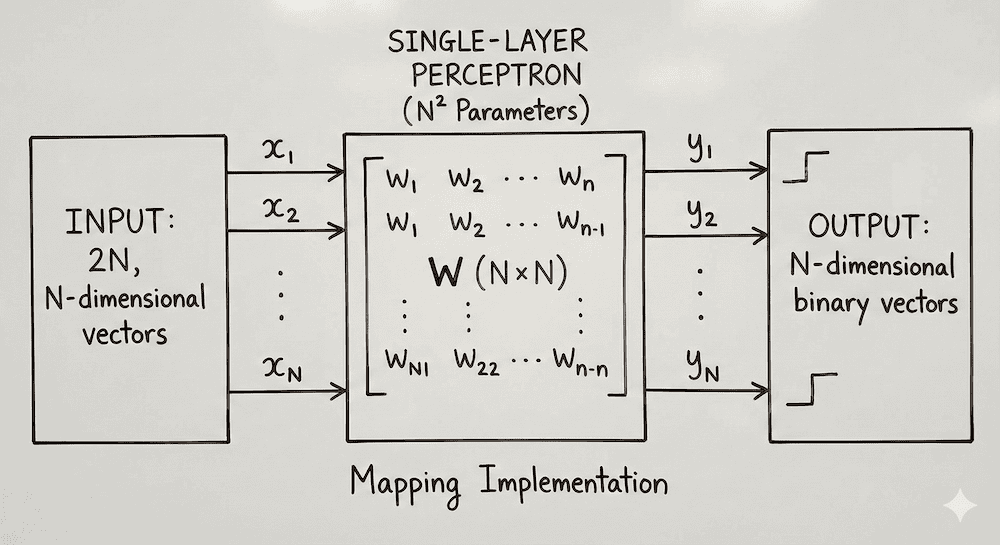
It is single-layer, so there are no intermediate (hidden) layers between the input nodes and the output nodes. Because it receives N dimensional vectors, and outputs N dimensional vectors we have 2N nodes with N X N (or N2) connections. Each of these connections has an associated weight, and it is these N2 weights that are our N2 “parameters”.
This is the network that can store 2 X N X N bits of information utilising N X N parameters.
2 bits of information per parameter
It is important to understand what it means for the neural network to store information, and it may be quite a foreign idea to those who are used to thinking of neural network’s ability to decide sentiment, recognise faces, or translate languages, rather than think about their relationship with the mathematical idea of information and its storage in parametric models like neural networks.
I will quickly give an intro to Information Theory, but see this from Stanford University for something more comprehensive.
Information exists in contrast to uncertainty. Given a unknown variable or set of variables, uncertainty is higher when it is ‘harder’ to predict the values of that variable/variable group. For example, a typical coin can be flipped and the outcome will be heads or tails. The outcome of the flip is the unknown variable; it is 50% likely to be heads and 50% likely to be tails. 2 possible outcomes.
A 8-sided die on the other hand has 8 equally possible outcomes. So for a die throw, predicting the value of the unknown variable is ‘harder’. How is this extra uncertainty quantified? Entropy is the equation that defines uncertainty. This is the equation for Entropy, where X is the uncertain outcome, and p(x) is the probability distribution over the values that outcome can take. In our examples things are simple, because all potential values of the outcome are equally likely.
Each outcome of the die throw has a probability of 1/8 so summing over each outcome in X we get 3 (it becomes -((1/8 * -3) + (1/8 * -3) + ...) ). The entropy of a die throw is 3. The entropy of a coin is 1, because we sum over two outcomes of probability 1/2. With outcome sets of equal probability, the entropy value is nice and clean, the logarithm (base 2) of the number of outcomes.
It was said before that information contrasts with uncertainty. To be specific, information is contained in that which reduces entropy. It is the thing that takes a variable which could be a number of ways, and reduces those number of ways such that we can more easily predict that variable. Most simply, if you can perfectly predict the outcome of an unknown variable, you have perfect information, and that information is precisely equal to the entropy of that random variable. If you have a variable space of K uncertainty, then to have the power to predict perfectly the values of that space is to have K information. This is crucial for soon understanding how each parameter has 2 bits of information.
Now there’s a subtle jump from saying “this random discrete variable has an entropy of 3” to saying “this random discrete variable has 3 bits of entropy. The unit “bits” comes entirely from the choice of logarithm base: using log base 2 means entropy is measured in bits. If we used natural logs, the entropy would be in nats; if we used log base 10, it would be in bans. We typically use bits because information theory and digital computation are built around binary encoding—not because the underlying math requires it.
So for our network to have 2 bits of information per parameter, 2 X N X N bits of information in total, it would have to provide perfect information of a variable space with 2 X N X N entropy. Like above, we assume that all outcomes are equally likely. This means that entropy is equal to the logarithm of the number of possible outcomes. Let B be the number of outcomes.
log2 B = 2 X N X N = 2N2
B = 22N2
That number gets big pretty quickly. At N = 100 we have:
B = 158426037257307868005973615116434779385850561749931084304089264171636965771228887445183221549634900407296411799021388514482539712212527560964434919010760105042125849116454433798935896220650780046807666431069499118740466866837959372847427258689339507115778715540823349866354881930899844372041800746660062647078769849898842814752322118795015775444493011299422019949776268167506192865779504464236743280761669197786530472490098079059778039682329847568790728044451902926135514328350694772562806871678146089186529664860081888383984871004699008224838580499751803515968006470065212530560848222545225611518763696038579381784537194800004157104657890526563726585544795235404652840413597055460523172340703162501727153461778559569316385319214984844854488705898953358474911000004317845656722556380177446898267540824349565051923332021650544761981831832447959514496708609116076028277050316882163176975111950192963213729930603362910401834553569223306295130504802504510333267498134802006070538650873017641896372875192828293321963152061479383675244933857476890220219901106655862535276130027150638410198329552070424997299107812369042423144903991740765446921500724419076751000298839481088892256273256063368929397432443933014214144749988527415844969725752903212470206761055261601849827654661699110625940038252592444127807711447974524104291407424843114880675244887296023580543784177280093241722370849027298852871426447848022843822902994734094797385919156612345556805228999781578857843967564419419389820652200704697216277604331475502184815154138578522599704839117099620440323976076189408437842592835693584440870980273228317430719718088417806011965249218133424685397314583877555043920477904186860401257506256394482324766380253922824732851857795933738539586533286494714037056888744575903707361945772578724435558330900806469646244239645951297065588493170705557002572646071293889342899884973471013547336074132058312069635733186787920170959871317410543537296985743086570399936143873193840643374631816914904860506917797431444238914497131049455649656508115021631292854300358556969140580788964452300041621575626091798586342244901878160798655296679261855611110073652803721254830922014932623403243155745232193950580851580911850733684806092512104808826053047325437803724154337434638903162568403492936621638617164329550798054121668806642220605470671206043129031608669748032306056358437105315978422234774926460517073989245245107819107854765567629692467190482389307528351002077335420019337555242527394307338870719127923956284961549495498790843593872752311823391339463516538283400267223543481963090012390530204516450554803984598953890817239000742556068802595920427778151959918090116862217516507638529119964994017518199856067593829858698164694379548113153767593100448607004918388327401892801427432297826759856964341637292026319148464168429714274957135079912049397318642781926160960990559408023450377550967128146636847975207536733868140822201431821054676744071472469699037765328909355841860295192771742323204868569121430751502931259791821245445709859916005187630403576001604005787864977303363066402561152710247206686262342396626030478513888796421963235041350325802452185758510209333111485659452918727076806529603424430454269446455756630217197847912013865363750346774090970145065574659477354372422254363041054990553133134795963757375352244526936032428066971967773792517860490850378585829410846140557461092179996153897741309684001675821933081194897521420112638349755677450652416434216421061269407213717720095189938797344341928856815077017462880322591391245465869672698126281313306113876047433685160012417576213516804723609783110561035013091058820942808166200834194018726856668841790429416742802104680185300791270851278776427023431533302663521354307567775557448772938508933920892066287027119642652300958465167090458635801843195210498211190913210321901142695584714344952503183763893110196124064914696259949340268324037113023594680716476379894628545317279904409379232735808639560672690096540624280404318683352778731415724742191076054728000279989743453367804496984328410450842940573462781082042215408423596863263148549613401913930196824033978848196722234139162366189919502087302034009115364953876499385538897537186573676382678158399152663344179370533450287905582746857120416965062438162120937264104028278768666160243784758041391265053015642423557836394416337448107620057878906244112952990434118093246924811270601497002602455762033134812497341331258587657058186258697629631241573869075154038890341453669819925327431348121974898693888115817829962206672674072982808675440812097158295778726322148681526519479030014867260060277979658621416827096378015776459215591554543373977417359449658238388364472141766283676832088648236424615713290767233613625291742713145813071396727380490010624790152355369710812209236293873831522879346461318242443971202942311144635310063794616933694427260120003016382186503059120517237756889959130570775741261586637799151582257917051213942427954042950164901050494611219168606113734439454603061628898982393998280676970344608876748458641750335811214876566237572767031075020462456127926968708186898126685739500550842578201345360630066084662471823273990020833543702484263518838822654965245517562276218952411178934717352443334239511247498011892977068051350106084618347697538036723468284914324127978903080794186533932834013575668784018726940097839567598461350388073254865816445489602424210267208612919113168904870677087973576763993287194899757891967902840989397230616059316453190544956322421787242379934006554206625156342315239175908415514540898703017989916939063280060183603935987407588531904499059854720097441237841042841670450316660441822462622753351205689006752551684077348869309983830110012144514135487108212085272167586802104801228293051152867522649774355434382686174550249127847895612860190159442886739115783259423932175318022892001985881700022097853203969988843558048556035582327550009998094312076218956668663403528162236623181598565920352728444224861865610692788036105430324074599854392872475129836852890733037381658915407354820626344793341766634507436537785710556280742554638210936803763367183717932460591183778499196311119794912856900178919549022959737636806806082561454811925248687822779948275663850775763453360225299664647308176835872234666655612540823001449360141673076532608560558121246539035021543073989172838706695228708932696061563871984374177564781016290210497367636877434031820920427967704482406511416736546272613393384567491473729794382476677368896597879109349189411856214468920530807981295394527120158216151212297452197673849811368802850436012971695681706372684272178023499099664970627727188232466668133905190084861986571933118283143830505003043161067804745622767906020390852846738800154692068177928929075173138848166306673947035138923269640863103574781393440967424278261714263530529402779936920333186963430474660672013897235011992105419321036332584885499518923161387972853536034915667139553228451271680734727075482453712313977117058649054205156812462247468357278658452864912590449585366204784811325353427040046376265449029961698861158291140003560411649046661208190466642543262325564715321710873906553590840048942536202204402107822429971993876850624164901685123950589980638245426051375536200108558064948694751933488887245308663404014695240961874513812799050066796102447526675711194363473815648826935317820768363954917529434481770353778066318002780955371243851611411236971676499260762878497746336235475825237247162264229016130864051710750247872168272378079981916215128442349160271304904006061407864288350946639799849760099927293832216326870598842379583972332301044249374243246293475841682249762335297428289119482175170422344063515671355050961556382786403421451994885943551709748812318379453091942108485765913396910136773681621453818001151727517439714067499739775535195304174251809822821768890995653291475922411950295782308657226659159356458543181426448271397875173489583442608961747633344819979116908814033427886937388498858106596068848164254210842941161627915068934821213720250703221346235164179985342633075077143552535479847480550427332004826388244691940872193177362938370585363597372432293627240433195975985122196212539785953642340059706881364100942607638561598051714392739028562476814989383094024455718813456095321164559494003137801634142271279332239289693158211838147338726652167673044867410715463242368202978701933845332426298534168256532589150715044751757801426429464213979087823326498711394307850162695685662034790323485598150518890234558995250334146105963843275800106995297594995691546815611222996123862259063127264941111090552368156446208226133416448201795477748160336962975627519707739895087176847519526417202028738530058803117633497104281880280094582529661507711017648388641662745078691751750141519880037443135338030504768309929145072306501892874489954596039809427879275707543043022253523744148560968026980566390565382539077665979141682498568225563247005480241699078160298538152812819275727570415916492241493546893198145554902488244519247184392645372309974742435004428382747165695755453322696293048385093775167761114904599666787743871148402482275693036219558360622691830701435183902464123516291964321521579186182546098255810688672477337443096972084318067161516059061332780329413144365459360664194287624589456757237464352565991547597175406782751635565081607698927632908541028185770190125817612467884164045179183520103588912617758508679654346661254504008296248458189615740661241309561469787327272532473463704301646423465794330671609942718581691560533989910798478501433092999182070347190905904203594251432241926482608142370175691905967084603989636644115054994021881643889240635512362421340370402585859315778051432283086869252853023328024327849828777352053136648246501866602791613031949526351559243244987855855938150238353890502211956086014543123980112838925943021029154997249978167418365020179016675405747769062555563363441037171593174477559950250467194754140307621766299677447047802262443256612096399355034105227446951230604760304628442668545355277453835271542666396714342529085987189927491291614609792009271279839396319037727357280499633288777893356815460210388520167956954388554485104439960116778601161722059873612474924229346012317124971881197255292462532555059514754082703407965655939226662440846262060929384066591323928205570748153548549753455390038246211989148391738608511740793108678262943694033603888664920510184608526616672478726912691104863229700330845906626510362263174852199278357891233378539052897158301758246855114986317573973013194210305768061139762501392406801181609925786910543702293811767693068875837746433794142362157582681531094658782207650254410358634904751054488872456434608346823657682138841885096733068433376046627710751254079793926395962238625754382799165084023395301182480569424557272338875335571969811814497172488163436863920485539394353051938789278945940242936792211707678272269328004369733847480992387784628669606195632880458362682964779591997959194324576535009082473611337678355955773547479127417419336519464323933976648117749192260816987404700021865418497897360646905978539618112555920935808868898404133204063618694711573982445416679851904343408976995328817583534524978356068733087497840435687832754634948353763292518019113464372532070256885205073992323715028537719271040755269721848977914699734957131184292129793413308667288624305122308161977853531870839921246045483766835926656216042449961960502865683335331024571534489835925521279010349412629838734521106652541959130016171617155773311289871451580846390585197740068502431924075742143748938629122191309954697068040259734692149485772250980290969211199204880588529717180139286749269934119742625668997996527398158826986395304249842478210131127802059281568541069198598556220361164491890944838074829823213149612629599385156901869544099427039617105487853132044072959452685496223920923518761160658310710890603281523682031568714797984572683670511849839021216518518243302351450146291740261419539404238142171912187124761482628312506044063402863471371850354986631677979187186458995889731181515366992121646799484887367079871289697795984721749551119434590853334711885025509376
Holy crap. So for a single-layer perceptron with input dimension 100 the uncertainty about the variable outcome is huge. The problem must be much more complicated that knowing the outcome of a 8-sided die roll. So where does this complexity come from?
a perceptron can implement a mapping from 2N, N-dimensional, input vectors to arbitrary N-dimensional binary output vectors…
Time to consider this bit of the passage. Fixing N at 5 for simplicity and brevity, we have our “arbitrary N-dimensional binary output vectors” looking like this [0, 1, 1, 1, 1] or this [0, 1, 1, 0, 0]. Each one of these output vectors can be one of 25 combinations. Thus the entropy of any single input-output pair is 5, the logarithm of the number of possibilities. Being able to know the outcome of a variable with 5 bits of entropy gives you 5 bits of information. Our network can supposedly implement a mapping for 10 (2N) of these, so the information of this network is 50 bits.
Where N = 5, number of outcomes (B) is 22N2 = 22*52 = 250. The entropy is thus 50, and so a neural network that can collapse the uncertainty about 10 5-dimensional binary vectors with an input->output mapping stores 50 bits. How many parameters are in this network? 5 * 5 = 25. So that’s 2 bits per parameter. Nice!
So this defines that criteria by which a neural network can be said to store information. It’s quite clear so far what the output vectors of this network look like, but what about it’s input? What is “general position” and why do the input vectors need to be in it?
More precisely, a perceptron can implement a mapping from 2N, N-dimensional, input vectors to arbitrary N-dimensional binary output vectors, subject only to the extremely weak restriction that the input vectors be in general position.
General Position is a very simple property of an input space that has important implications for the storage capacity of the neural network. Because we’ve seen that information can be stored in the network by implementing mappings from some input vector to a binary output vector, the amount of mappings possible within the network has direct impact on capacity. So it turns out that whether or not a neural network can map 2N inputs to arbitrary binary outputs depends also on the input vector group and not just on the architecture of the network.
General position can be a characteristic of any set of points or geometric objects, but let’s first consider a small set of low-dimensional vectors, and a more simple single-layer perceptron that maps inputs to either 0 or 1. In order to implement a mapping from inputs to outputs, a single-layer perceptron network must obviously implement a function. In our simple case this function determines a dichotomy; points are either 0 or they’re 1.
(Note: The network under discussion here has no ‘bias value’ for simplicity, but ignoring that does not compromise generality)
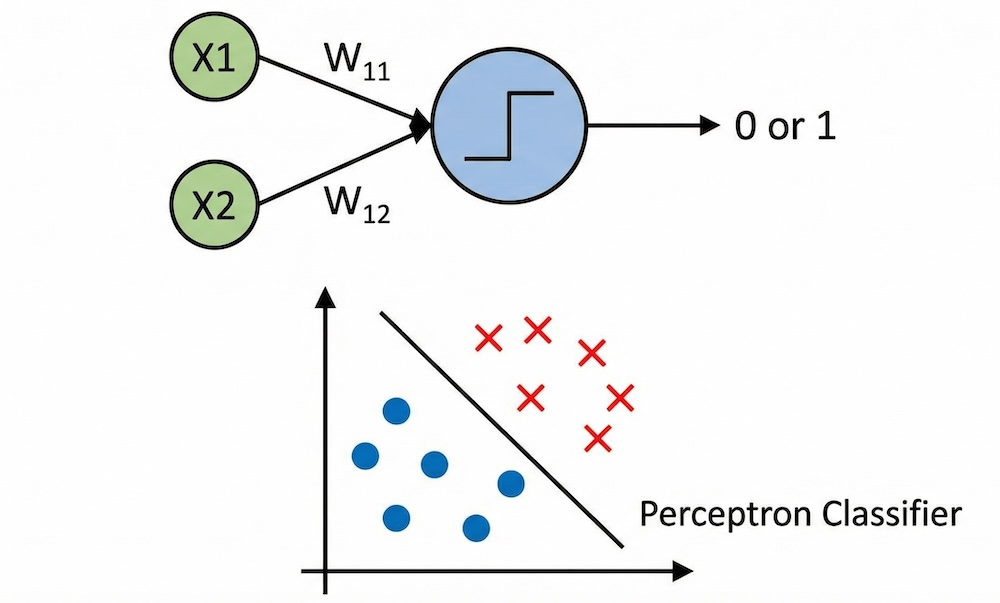
Our small set of low-dimensional vectors looks like this: {[0,1], [2, 2], [0,5]}. These 3 vectors with dimension N = 2 could map to one of 8 possible outcomes: [0,0,0], [0,0,1], [0,1,0] ... [1, 1, 1]. The entropy of this variable space is thus 3 (log223). The function of our neural network must be able to dichotomise these 3 points in those 8 ways. If it doesn’t, then it hasn’t completely removed the entropy of the variable space, and thus can’t claim the full 3 bits of information.
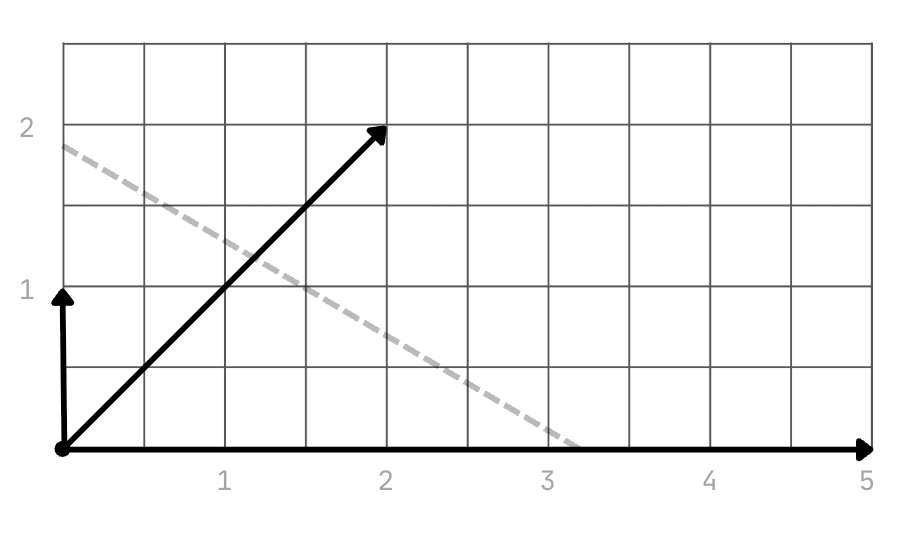
What happens though if we change [0, 5] to [4, 4]? Our new set becomes {[0,1], [2, 2], [4,4]} and our plot looks like this:
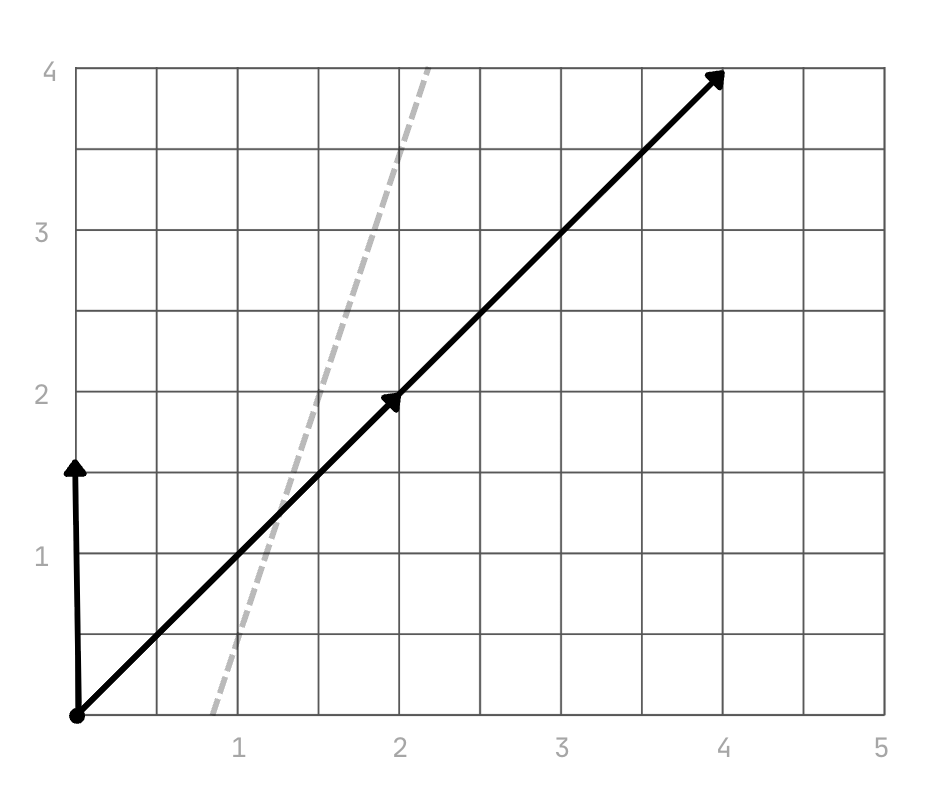
It should be quite clear that the network can no longer implement functions that dichotomise the 3 inputs in 8 different ways. Imagine trying to drawing a line that separates (dichotomises) these vectors. Our new input space has imposed a restriction on the network such that it cannot implement a mapping to “arbitrary [2]-dimensional binary output vectors”. This directly impacts the information storage capacity of the network because the linear dependence of [2, 2] and [4, 4] ensure that they must share the same outcome. If they share an outcome, then the uncertainty about the system is reduced.
Now it was called an “extremely weak restriction”, this need for general positionality. Why? Well, because in some space d dimensional space it is almost certain that any random set of real valued points from d will be in general position. You’d have to carefully design your variable space to not have this quality.
This idea of a variable space having a ‘complexity’ that enables a neural network to implement the full complement of possible dichotomies can be solidified by further reading into Cover’s Function Counting Theorem.
Exactly how a neural network’s group of weights is able to implement these arbitrary function mappings is outside the scope of this blogpost. Maybe I’ll do it in a follow-up. If you want to go into yourself, the “Perceptron Learning Algorithm” is explored under heading 3 in Introduction: The Perceptron, Haim Sompolinsky, MIT.
“At least 2”
Now there’s one last thing to note about the quote introduced at the start. It says “at least” 2 bits. So it can be more? For a quick answer let’s dip into one of the physics papers linked in our top quote, The Space of Interactions in Neural Network Models - E Gardner, Dep. of Physics, Edinburgh University.
In the random case, the maximum number of patterns is 2N (Cover 1965, Venkatesh 1986a, b, Baldi and Venkatesh 1987) and we will show that this increases for correlated patterns. [emphasis mine]
For random patterns, the storage capacity is 2 bits, but when input patterns are correlated, the network is able to exploit the correlation to store more pattern -> output mappings. The correlation between inputs means that the storage of each individual pattern represents less information storage, but overall the storage capacity of the network is increased beyond 2 bits per parameter because of a relatively larger increase in the number of stored patterns. I don’t understand that physics paper very well at all, and its exploring neural networks in an unfamiliar context where apparently “magnetism -> m” is a thing, but I think the high-level intuition can be gathered.
References
- Introduction to Information Theory
- Information Theory, Inference, and Learning Algorithms - David J.C MacKay
- Capacity and Trainability in Recurrent Neural Networks - Arxiv.com
- Introduction: The Perceptron Haim - Haim Sompolinsky, MIT (October 2013)
- Physics of Language Models: Part 3.3, Knowledge Capacity Scaling Laws (April, 2024)
- Capacity and Trainability in Recurrent Neural Networks (ICLR 2017)